Da Wikipedia, l'enciclopedia libera:

Localmente la superficie terrestre sembra piatta e assomiglia ad un
piano, ma in realtà è incurvata. In matematica, un oggetto di questo
tipo è una varietà di dimensione 2. Gli effetti della curvatura
possono essere misurati calcolando la somma degli angoli interni di un
triangolo: nel piano è sempre 180°, ma su una sfera è maggiore, ad
esempio 90°+90°+50° = 230° in figura.
Esempi di varietà sono le curve e le superfici. L'universo è intuitivamente un esempio di varietà tridimensionale. La relatività generale descrive lo spaziotempo come una varietà con 4 dimensioni.
Quale nozione di varietà
L'idea di "spazio a più dimensioni" è descritta e studiata in vari modi differenti, fra loro correlati. Usando gli strumenti della topologia, del calcolo infinitesimale, dell'analisi complessa e dell'algebra si arriva rispettivamente ai concetti di varietà topologica, varietà differenziabile, varietà complessa e varietà algebrica.Concetti più raffinati come quello di curvatura vengono definiti nell'ambito della geometria differenziale, e portano ad esempio alla nozione di varietà riemanniana.
Varietà topologica

La circonferenza è una varietà topologica di dimensione 1. Qui è descritto un atlante con quattro carte: ciascuna è un omeomorfismo fra un aperto ed un intervallo aperto di 

Una varietà topologica modella uno spazio
 -dimensionale dal punto di vista topologico: si definiscono quindi solo le proprietà di base dello spazio, che ne caratterizzano esclusivamente la forma.
-dimensionale dal punto di vista topologico: si definiscono quindi solo le proprietà di base dello spazio, che ne caratterizzano esclusivamente la forma.Definizione formale
Una varietà topologica di dimensione è uno spazio topologico di Hausdorff
è uno spazio topologico di Hausdorff  in cui ogni punto ha un intorno aperto omeomorfo ad un aperto dello spazio euclideo
in cui ogni punto ha un intorno aperto omeomorfo ad un aperto dello spazio euclideo  -dimensionale
-dimensionale  . Il numero
. Il numero  è la dimensione della varietà.
è la dimensione della varietà.Un omeomorfismo fra un aperto di
 e un aperto di
e un aperto di  è detto una carta. Quindi
è detto una carta. Quindi  è una varietà topologica se esiste un insieme di carte che ricoprono tutto
è una varietà topologica se esiste un insieme di carte che ricoprono tutto  . Un insieme di carte di questo tipo è un atlante. I nomi "carta" e "atlante" sono scelti in analogia con gli atlanti planetari: infatti la superficie della Terra non è descrivibile interamente su un foglio (cioè, non è omeomorfa ad un aperto di
. Un insieme di carte di questo tipo è un atlante. I nomi "carta" e "atlante" sono scelti in analogia con gli atlanti planetari: infatti la superficie della Terra non è descrivibile interamente su un foglio (cioè, non è omeomorfa ad un aperto di  )
però è possibile descriverla "a pezzi", tramite un certo numero di
carte geografiche, ciascuna delle quali descrive solo una zona della
superficie: ad esempio, con due carte che descrivono gli emisferi Nord e Sud.
)
però è possibile descriverla "a pezzi", tramite un certo numero di
carte geografiche, ciascuna delle quali descrive solo una zona della
superficie: ad esempio, con due carte che descrivono gli emisferi Nord e Sud.Una varietà di dimensione
 è spesso chiamata brevemente
è spesso chiamata brevemente  -varietà.
-varietà.Esempi

La bottiglia di Klein: ogni "quadratino" è contenuto in una carta bidimensionale.
Dimensioni basse
La topologia della dimensione bassa è la branca della topologia che studia le varietà di dimensione fino a 4.Esistono praticamente solo due varietà topologiche di dimensione 1, la circonferenza e la retta: ogni altra varietà di dimensione 1 è infatti omeomorfa a una di queste due. Le varietà di dimensione 2, chiamate superfici, sono invece infinite e più variegate. Tra queste troviamo ad esempio già molti esempi notevoli dal punto di vista topologico: la sfera, il toro, il nastro di Möbius, la bottiglia di Klein.
La bottiglia di Klein è un esempio importante: benché sia "localmente" un oggetto bidimensionale, non è realizzabile "globalmente" come sottoinsieme né del piano né dello spazio (ma è realizzabile dentro lo spazio
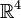 quadri-dimensionale!).
quadri-dimensionale!).Una varietà di dimensione 3 intuitivamente è un oggetto che "potrebbe essere" l'universo in cui viviamo. Le 3-varietà non sono facilmente visualizzabili, ed il loro studio è una branca importante della topologia. La congettura di Poincaré, dimostrata nel 2003 da Grigori Perelman, è stato un importante problema irrisolto per più di un secolo, riguardante proprio questo ambito.
Una varietà di dimensione 4 è un oggetto ancora più difficile da visualizzare. Lo studio delle varietà con quattro dimensioni è un punto centrale della matematica moderna, con numerosi collegamenti alla fisica teorica: la relatività generale descrive infatti lo spaziotempo come una 4-varietà.
Superfici sferiche
Una superficie sferica di dimensione arbitraria è sempre una varietà
arbitraria è sempre una varietà  -dimensionale. Essa è definita come il luogo dei punti in
-dimensionale. Essa è definita come il luogo dei punti in  che soddisfano l'equazione
che soddisfano l'equazione e
e  . La proiezione stereografica descrive due carte, ciascuna contenente uno dei due emisferi.
. La proiezione stereografica descrive due carte, ciascuna contenente uno dei due emisferi.Varietà differenziabile
| Per approfondire, vedi Varietà differenziabile. |
Una varietà differenziabile è definita come una varietà topologica, le cui funzioni di transizione sono però differenziabili (e non solamente continue come nel caso topologico).
Se le funzioni di transizione sono in più analitiche, la struttura risultante si chiama una varietà analitica.
Varietà complessa
| Per approfondire, vedi Superficie di Riemann. |
Una varietà complessa è definita come una varietà topologica di dimensione
 , le cui funzioni di transizione, viste come mappe fra aperti di
, le cui funzioni di transizione, viste come mappe fra aperti di 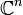 tramite l'identificazione naturale di
tramite l'identificazione naturale di  con
con 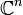 , sono però olomorfe.
, sono però olomorfe.Poiché le funzioni analitiche sono differenziabili, una varietà complessa ha anche una struttura di varietà differenziabile.
Varietà algebrica
| Per approfondire, vedi Varietà algebrica. |
Una varietà algebrica è un oggetto che è localmente definito come l'insieme degli zeri di uno o più polinomi con
 variabili in
variabili in  , dove
, dove  è un campo fissato, come ad esempio il campo dei numeri reali o complessi. Gli esempi più semplici di varietà algebriche sono le varietà affini e le varietà proiettive.
è un campo fissato, come ad esempio il campo dei numeri reali o complessi. Gli esempi più semplici di varietà algebriche sono le varietà affini e le varietà proiettive.
Varietà affini in  definite da alcuni semplici polinomi in due variabili: due circonferenze, una parabola, una iperbole, una cubica (definita da un'equazione di terzo grado).
definite da alcuni semplici polinomi in due variabili: due circonferenze, una parabola, una iperbole, una cubica (definita da un'equazione di terzo grado).
 definite da alcuni semplici polinomi in due variabili: due circonferenze, una parabola, una iperbole, una cubica (definita da un'equazione di terzo grado).
definite da alcuni semplici polinomi in due variabili: due circonferenze, una parabola, una iperbole, una cubica (definita da un'equazione di terzo grado).Varietà affine
| Per approfondire, vedi Varietà affine. |
 di
di  che è il luogo di zeri di un insieme
che è il luogo di zeri di un insieme  di polinomi in
di polinomi in  variabili. In altre parole,
variabili. In altre parole,  è l'insieme dei punti su cui si annullano contemporaneamente tutti i polinomi in
è l'insieme dei punti su cui si annullano contemporaneamente tutti i polinomi in  , cioè
, cioè  è l'insieme delle soluzioni di un sistema di equazioni polinomiali. Generalmente si indica
è l'insieme delle soluzioni di un sistema di equazioni polinomiali. Generalmente si indica  per rimarcare la dipendenza di
per rimarcare la dipendenza di  dall'insieme
dall'insieme  .
.I polinomi in
 non devono necessariamente essere in numero finito. Se
non devono necessariamente essere in numero finito. Se  è l'ideale generato da
è l'ideale generato da  , risulta che
, risulta che 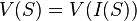 : quindi ogni varietà è in verità il luogo di zeri di un ideale di polinomi. L'importanza degli ideali nella teoria degli anelli discende proprio da questo fatto.
: quindi ogni varietà è in verità il luogo di zeri di un ideale di polinomi. L'importanza degli ideali nella teoria degli anelli discende proprio da questo fatto.Varietà proiettiva
| Per approfondire, vedi Varietà proiettiva. |
 dello spazio proiettivo
dello spazio proiettivo  , definito analogamente alla varietà affine come luogo di zeri di un insieme
, definito analogamente alla varietà affine come luogo di zeri di un insieme  di polinomi. L'unica differenza con il caso affine sta nel fatto che tali polinomi hanno
di polinomi. L'unica differenza con il caso affine sta nel fatto che tali polinomi hanno  variabili, e poiché le coordinate omogenee di un punto nello spazio proiettivo sono definite a meno di una costante moltiplicativa, questi devono essere omogenei affinché le equazioni abbiano senso.
variabili, e poiché le coordinate omogenee di un punto nello spazio proiettivo sono definite a meno di una costante moltiplicativa, questi devono essere omogenei affinché le equazioni abbiano senso.Varietà riemanniana
| Per approfondire, vedi Varietà riemanniana. |
In particolare una varietà riemanniana è uno spazio metrico, su cui è definito il concetto di geodetica come curva che realizza localmente la distanza fra due punti. Su una varietà riemanniana sono quindi presenti tutti gli enti geometrici classici della geometria euclidea, benché il loro comportamento possa differenziarsi enormemente dal comportamento degli usuali enti nel piano: ad esempio può non valere il V postulato di Euclide, né altri assiomi di Hilbert. Localmente, questa differenza di comportamento è misurata dalla curvatura della varietà riemanniana. Globalmente, è dovuta alla topologia della varietà.
Esempi di varietà riemanniane sono le sottovarietà dello spazio euclideo
 . La sfera
. La sfera  -dimensionale in
-dimensionale in  è un esempio fondamentale di varietà riemanniana con curvatura
positiva. Lo spazio euclideo ha invece curvatura nulla. Uno spazio
importante con curvatura negativa è il disco di Poincaré: si tratta dell'usuale palla in
è un esempio fondamentale di varietà riemanniana con curvatura
positiva. Lo spazio euclideo ha invece curvatura nulla. Uno spazio
importante con curvatura negativa è il disco di Poincaré: si tratta dell'usuale palla in  , su cui è però definita una metrica diversa da quella euclidea.
, su cui è però definita una metrica diversa da quella euclidea.Origine del termine
| Per approfondire, vedi Aggettivo numerale#Etimologia e paralleli. |
Analizzando il termine come parola composta, Mannig-faltig-keit, si riconosce in essa un parallelo con il termine latino multi-plic-itas, sicché lo si potrebbe tradurre letteralmente come 'molteplicità'.
Note
- ^ In inglese i nomi variety e manifold sono usati rispettivamente per le varietà algebriche e quelle topologiche, differenziabili o complesse.

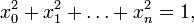

Nessun commento:
Posta un commento
Salve, donatemi un pò dei Vostri Pensieri: